Important

This is Version 2 of Lab 7 Rehearse 2. If you need the original version, it is here

Link to Posit Cloud

Log into your Posit Cloud account.
Open the Lab 7 Hypothesis Tests 2 workspace.
Open the Lab-7-Rehearse2-Worksheet.Rmd.

Note that you will do all your work for this rehearse in the Lab-7-Rehearse2-Worksheet.Rmd. Click on that file to open it in the Source/Editor window in your Posit Cloud Lab 7 Hypothesis Tests 2 workspace.

IMPORTANT!

Remember to rename this file to include your name in place of “Student-Name” at the top of the page.

Other than entering your name to replace Student Name and changing the date to the current date, do not change anything in the head space.

Samples with Multiple Proportions

Introduction

In the first rehearse of module 7, we learned how to compare a single proportion found in one sample to a standard or assumed value. And to compare the single proportions found in two samples to each other.

But what do we do when we have more than two proportions in a sample to compare?

Of course, we have a test for that situation. And it is an oldie but a goodie.

In fact, the test we use is one of the oldest hypothesis tests which was invented by Karl Pearson around the turn of the century, the goodness of fit test which uses the Chi-squared distribution instead of the normal or t distributions we have previously discussed.

But don’t worry.

We are not going to get deep into theory here, but just let R do the background work for us again.

One Categorical Variable: Goodness of Fit Test

A particular brand of candy-coated chocolate comes in five different colors: brown, coffee, green, orange, and yellow. The manufacturer of the candy says the candies colors are distributed in the following proportions in each package: brown - 40%, coffee - 10%, green - 10%, orange - 20%, and yellow - 20%.

A random sample of 600 pieces of this candy is collected. Does this random sample provide sufficient evidence against the manufacturer’s claimed distribution of colors that we can conclude the actual distribution of the proportions of colors is different.

We will answer this question using the Downey/Infer process.

Load Packages

First load the necessary packages:

CC1

library(tidyverse)
library(infer)

Get Familiar with the Data

Load the data

The following code chunk will read in the data:

CC2

# The read.csv function is found in the 'readr' package which # is automatically loaded as part of the 'tidyverse' package.

# this code will load the required data file from your workspace /data folder.

candies <- read.csv("./data/candies02.csv")

#This displays the data object 'candies'
head(candies) #shows the first 6 rows

##   color_
## 1  brown
## 2  brown
## 3  brown
## 4  brown
## 5  brown
## 6  brown

You should see the candies data object in the Environment.

There is one categorical variable, color_.

Exploratory data analysis

Find unique colors of candy

We can display the levels of that variable using the following code. By “levels” we mean unique values of color in the column of data.

CC3

# Display the levels of the categorical variable 'color_'

unique(candies$color_)

## [1] "brown"  "coffee" "green"  "orange" "yellow"

So, we have five different colors of candy.

Find the counts

We can find the counts of the number of candy pieces of each color.

CC4

# This code creates a table that summarizes the numbers of each color.
color_count <- table(candies$color_)
# This displays the table.
color_count

## 
##  brown coffee  green orange yellow 
##    234     60     48    132    126

Find the proportions

We can also calculate the proportions of each color in the sample data.

CC5

obs_prop <- prop.table(table(candies$color_))
#display the table of proportions of the candy colors in the sample.
obs_prop

## 
##  brown coffee  green orange yellow 
##   0.39   0.10   0.08   0.22   0.21

These are the proportions of the colors stated by the manufacturer: brown - 40%, coffee - 10%, green - 10%, orange - 20%, and yellow - 20%.

Knowledge Check

Are there differences in the stated and the observed proportions?

Your answer here:

Make a guess: are these differences between the stated and observed proportions statistically significant?

Your answer here:

Visualize the data

In the following code chunk, we create a bar chart to display the count of the number of M&M’s of each of the stated colors in the dataset candies.

CC6

ggplot(data = candies, aes(x = color_, fill = color_)) +
  geom_bar()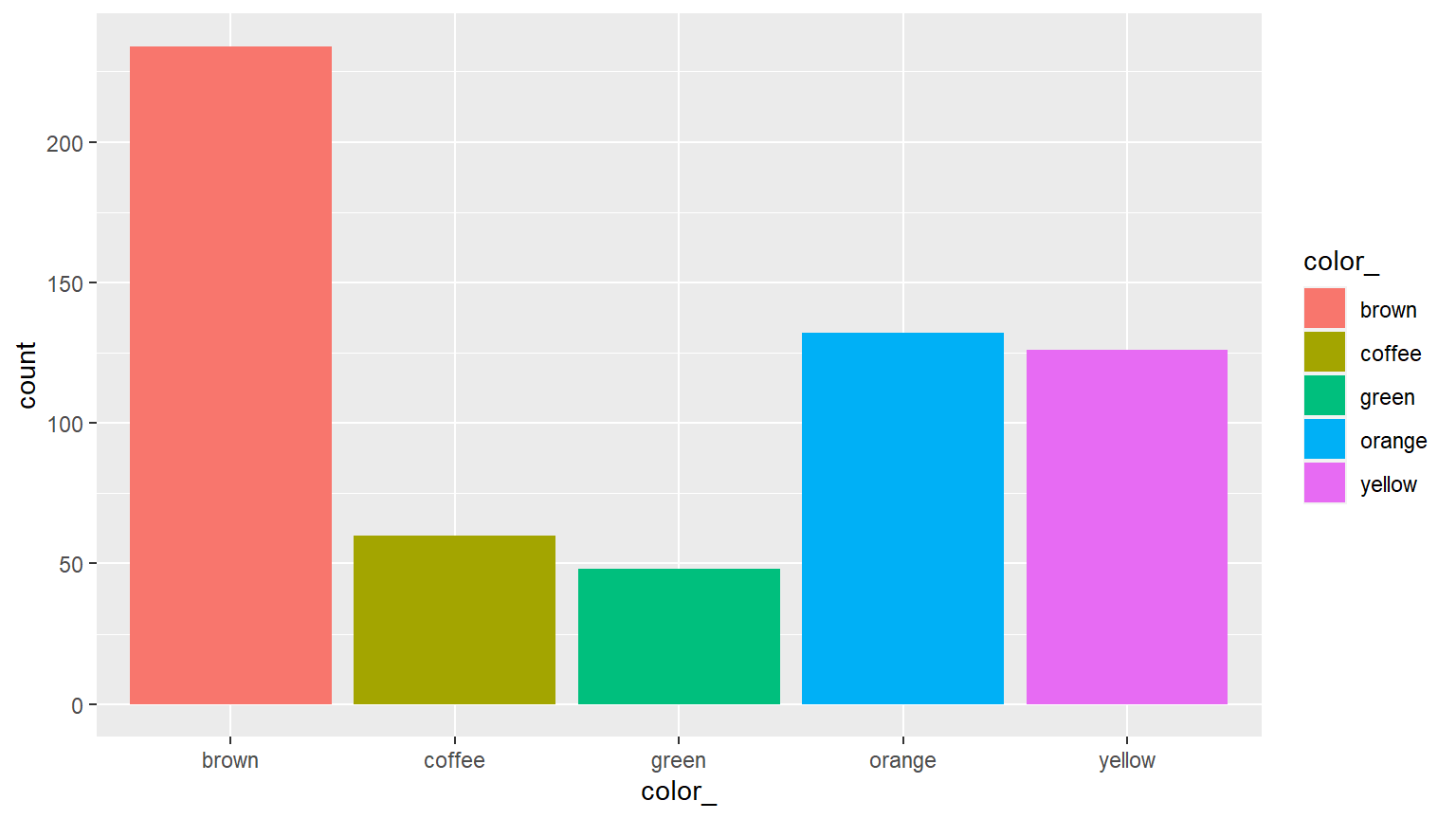

Note that in the last code chunk we allowed R to select the colors to be displayed. That is why most of the colors do not match the actual color names.

We can use standard codes for the colors, called “hex codes.” There are several places where you can get the hex codes. Here is one site that has several easy to use ways to pick color code: (https://htmlcolorcodes.com/){target=“_blank”}

We used this page to pick the brown and coffee color hex codes: (https://htmlcolorcodes.com/colors/shades-of-brown/){target=“_blank”}

CC6a improved version

We just added another line of code using the ggplot + to “manually” specify the colors to use.

CC6a

ggplot(data = candies, aes(x = color_, fill = color_)) +   geom_bar() +
  scale_fill_manual(values=c("#8B4513", "#6F4E37", "#50C878", "#FFAC1C", "#FFEA00")) +
labs(title = "Distribution of Candy Colors in Sample", 
       x = "Candy Color", y = "Count of Candies")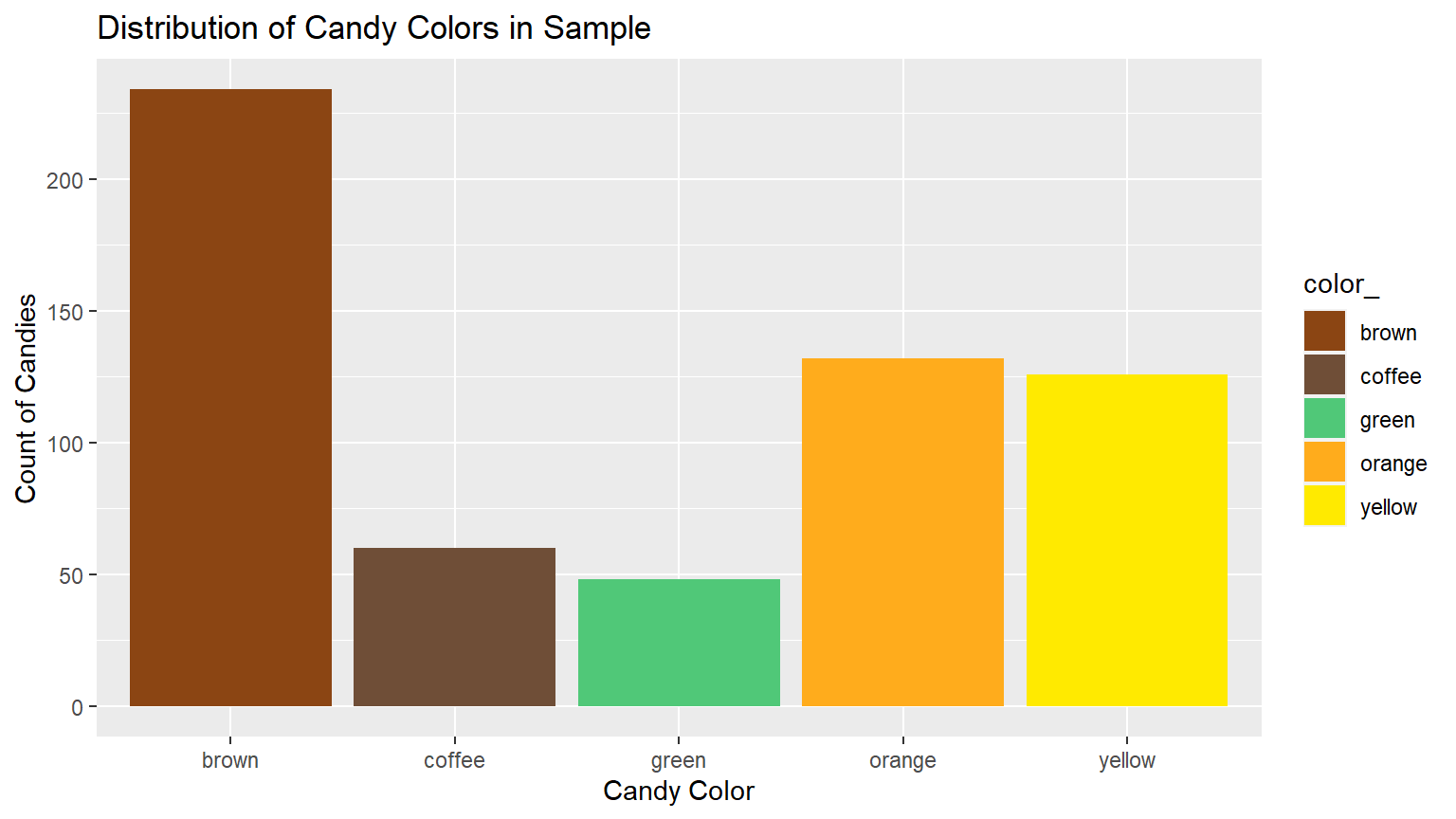

Do not include the next data visualization in the Remix submission.

This next visualization is used in this example to provide a bit more clarity to the problem.

But you do not need to include this data viz in your Remix Goodness of Fit question. You do not need to try to “wrangle” the provided data sets for the Remix research questions.

We could make more sense of the problem if we could visualize the stated and observed proportions together. So, we wrangled the original data to create a special data set to create a stacked bar chart to better illustrate the Planned and Observed proportions of colors of candies. We will use it for this chart only.

CC7

# load the special data
candies2 <- read.csv("./data/candies2.csv")
# create a side by side bar plot
candies2 %>% ggplot(aes(x = group, fill = color_)) +
  geom_bar(position = "fill") +
  #the values are the "Hex" codes for brown, coffee, green, orange, and yellow.
  scale_fill_manual(values=c("#8B4513", "#6F4E37", "#50C878", "#FFAC1C", "#FFEA00")) +
  ylab("Proportion") +
  xlab("Observed vs Planned Proportions") +
  ggtitle("Proportions of Colors")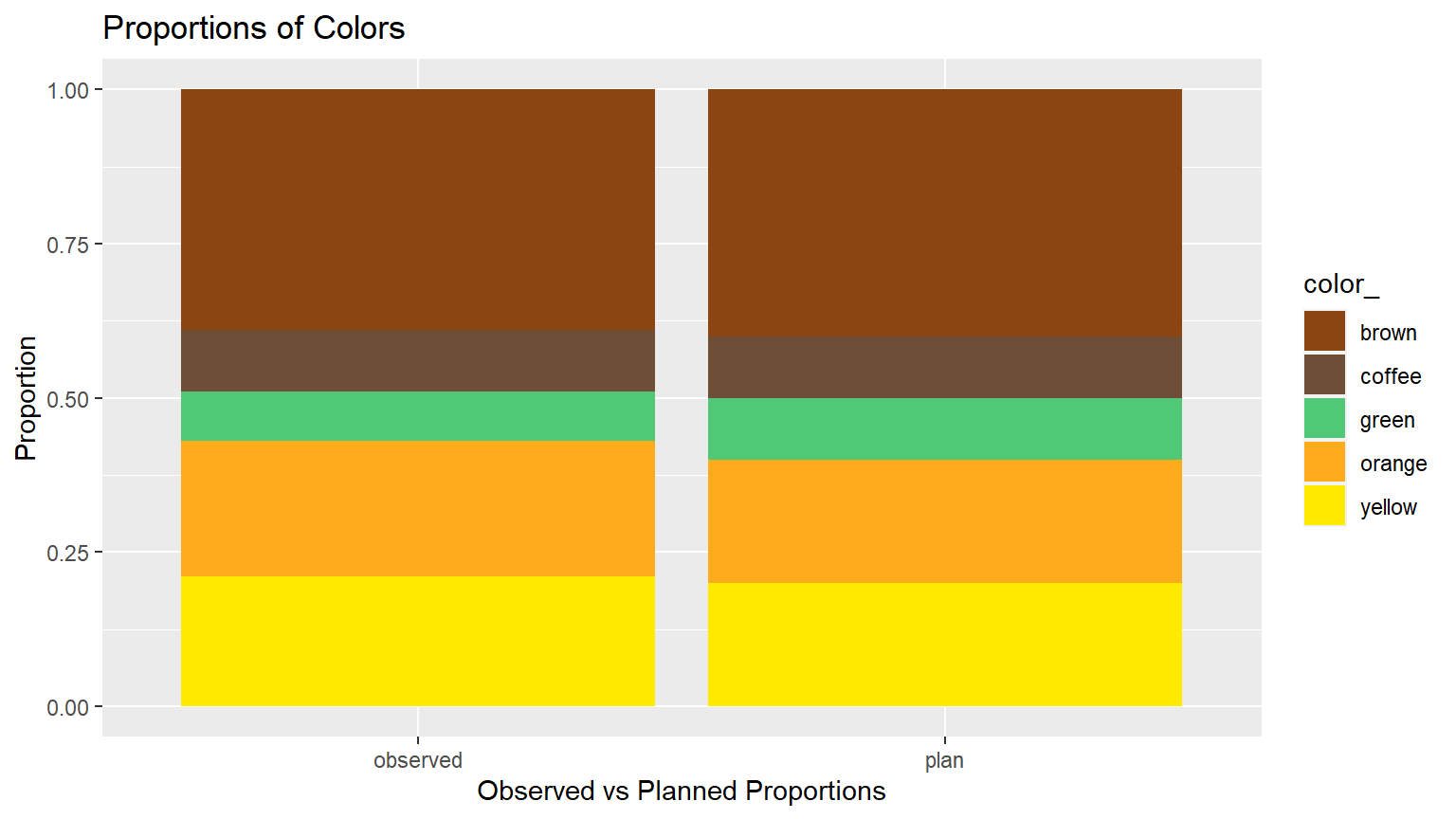

Knowledge Check

What is your opinion about the difference in the two sets of proportions now?

Your answer here:

State the Null and Alternative hypotheses

Null hypothesis Ho: The true proportions of a particular brand of candy-coated chocolate in the sample match what the manufacturer states: brown - 40%, coffee - 10%, green - 10%, orange = 20%, and yellow - 20%.

Alternative hypothesis Ha: The distribution of candy proportions observed in the sample differs from what the manufacturer states.

State the Significance Level

It’s important to set the significance level “alpha” before starting the testing using the data.

Let’s set the significance level at 5% ( i.e., 0.05) here because nothing too serious will happen if we are wrong. (we are not going to publish our results!)

Testing the hypothesis

Here’s how we use the Downey method with infer package to conduct this hypothesis test:

Step 1: Calculate the observed statistic

Calculate the observed statistic delta and store the results in a new data object called delta_obs.

We use the Chi-square statistic for our difference Delta.

Note that we use a “point” null even though we have five values - they are all point values.

It is important that the sum of the proportions values add up to exactly 1.

CC8

delta_obs <- candies %>%
# specify response variable
   specify(response = color_) %>%
# use the planned values here, not the observed proportions 
# the planned values will be compared to the response variable color_
  hypothesize(null = "point",
              p = c("brown" = 0.4,
                    "coffee" = 0.1,
                    "green" = 0.1,
                    "orange" = 0.2,
                    "yellow" = 0.2)) %>%
  calculate(stat = "Chisq")


#Display out the results
delta_obs

## Response: color_ (factor)
## Null Hypothesis: point
## # A tibble: 1 × 1
##    stat
##   <dbl>
## 1  4.05

Our observed difference Delta equals a Chi-square value of 4.05.

Step 2: Generate the Null Distribution

Generate the null distribution of the difference delta.

CC9

#set seed for reproducible results
set.seed(123)

#create the null distribution
null_dist <- candies %>%
#specify response variable
   specify(response = color_) %>%
#use the Null proportions here
  hypothesize(null = "point",
              p = c("brown" = 0.4,
                    "coffee" = 0.1,
                    "green" = 0.1,
                    "orange" = 0.2,
                    "yellow" = 0.2)) %>%
  #the next line is added to generate the 1000 reps for the Null Distribution
  generate(reps = 1000, type = "draw") #%>%

Step 3: Calculate the Null difference

CC10

# create a new data object `null_delta` to hold the differences
# in the Null world.

null_delta <- null_dist %>% 
  calculate(stat = "Chisq")

Step 4: Visualize the Null and the Delta

Visualize how the observed difference compares to the null distribution of delta.

The following plots the delta values we calculated for each of the different “shuffled” replicates.

This is the null distribution of delta.

The red line shows the obs_stat which is the value of delta_obs from CC8.

Unlike the difference in means we previously worked with, the Chi-square test is only a right tail test.

CC11

visualize(null_delta) +
#Note the Chi-square test is always a right-tail test
  shade_p_value(obs_stat = delta_obs, direction = "greater")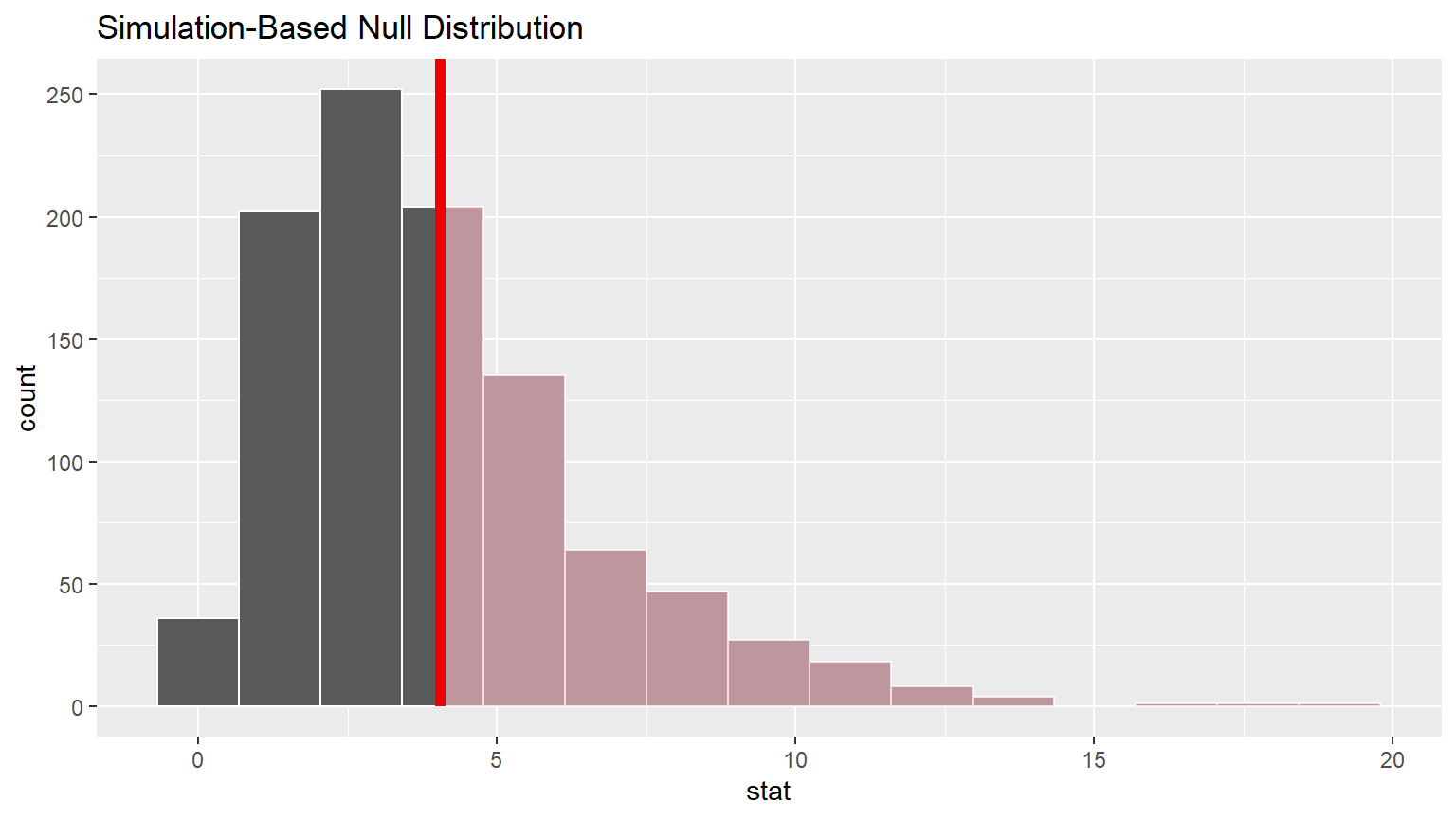

The observed test statistic of 4.05 does not appear to be in the “tail” of the null distribution and thus is not unusual.

Remember that the “pinkish” shaded portion of the distribution represents the area under the “curve” and thus the probability of getting an as extreme (extreme means ‘large value’ since the Chi-square test is always a right-tail test) or even more extreme delta - i.e. the p-value.

Important concept:

Note that because the red line delta_obs is NOT in an extreme tail of the distribution, it does occur often in the Null world.

Step 5: Calculate the p-value

Calculate the p-value (“area” under the curve beyond delta_obs) from the Null distribution and the observed statistic delta_obs.

CC12

null_delta %>%
  get_p_value(obs_stat = delta_obs, direction = "greater")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1   0.409

Step 6: Results and Conclusions

Because the p-value of 0.409 is not less than the significance level of 0.05, we cannot reject the Null Hypothesis on no difference.

Therefore we conclude that the observed distribution of proportions of candy colors is the same as the planned distribution of proportions of candy colors.

Step 7: Calculate confidence interval

The confidence interval approach is not used for Chi-square tests.

Step 8: Traditional hypothesis test

CC13

chisq_test(candies,
  response = color_,
  p = c("brown" = 0.4,
        "coffee" = 0.1,
        "green" = 0.1,
        "orange" = 0.2,
        "yellow" = 0.2))

## # A tibble: 1 × 3
##   statistic chisq_df p_value
##       <dbl>    <dbl>   <dbl>
## 1      4.05        4   0.399

By inspection, you should notice the results of the two methods are relatively similar.

But to use the traditional (formula-based, theoretical) Chi-square test there are several assumptions which must be checked:

Independent observations: The observations are collected independently. The cases are selected independently through random sampling so this condition is met.
Expected cell counts: All expected cell counts are at least 5.
- 580 * 0.1 = 58 and since 0.1 is the smallest expected proportion, this condition is met.
Degrees of freedom: The degrees of freedom must be at least 2. There are five different groups of candy colors here so our degrees of freedom is 4.

Note: you do not need to actually check the assumptions of the traditional test for this course.

Two Categorical Variables: Test for Independence

Recall in Module 4, we looked for a relationship, a correlation, between two quantitative variables, such as height and shoe size. If we have a sufficient sample, we can first make a scatter plot to look for a “trend” in the pattern of dots, the data points. And we can plot a best fit line to help us see the trend more easily. If the line is sloping up from left to right, we have a positive correlation: as the x-variable increases, the y-variable increases. If the line slopes downward from left to right, we have a negative correlation: as x increases, y decreases. And, of course, we can have a situation in which there is no relationship, no obvious trend either way.

We can also look for a relationship between two categorical variables using another Chi-square test, the Test for Independence.

Problem Statement A random sample of 500 U.S. adults was questioned regarding their political affiliation (democrat or republican) and opinion on a tax reform bill (favor, indifferent, opposed).

Based on this sample, do we have reason to believe that political party and opinion on the bill are related?

Load Packages

First load the necessary packages:

CC14

library(tidyverse)
library(infer)

Get Familiar with the Data

Load the data

CC15

tax500<- read.csv("./data/tax500.csv")

Exploratory data analysis

Find the counts

CC16

# Use the table function to create the table
counts <- table(tax500$opinion, tax500$party)

counts

##              
##               Democrat Republican
##   Favor            138         64
##   Indifferent       83         67
##   Opposed           64         84

Find the proportions

We can also calculate the proportions in the sample data.

CC17

# Calculate proportions in each column (ie the party affiliation)
# Using the round function to round the values to 3 decimals
proportions <- round(counts / colSums(counts), 3)

# Print the resulting table
proportions

##              
##               Democrat Republican
##   Favor          0.484      0.298
##   Indifferent    0.386      0.235
##   Opposed        0.225      0.391

Visualize the Data

We will next generate a data visualization that displays the total SAT scores of the two groups.

CC18

tax500 %>% ggplot(aes(x = party, fill = opinion)) +
  geom_bar(position = "fill") +
  ylab("Proportion") +
  xlab("Party") +
  ggtitle("Opinion by Party")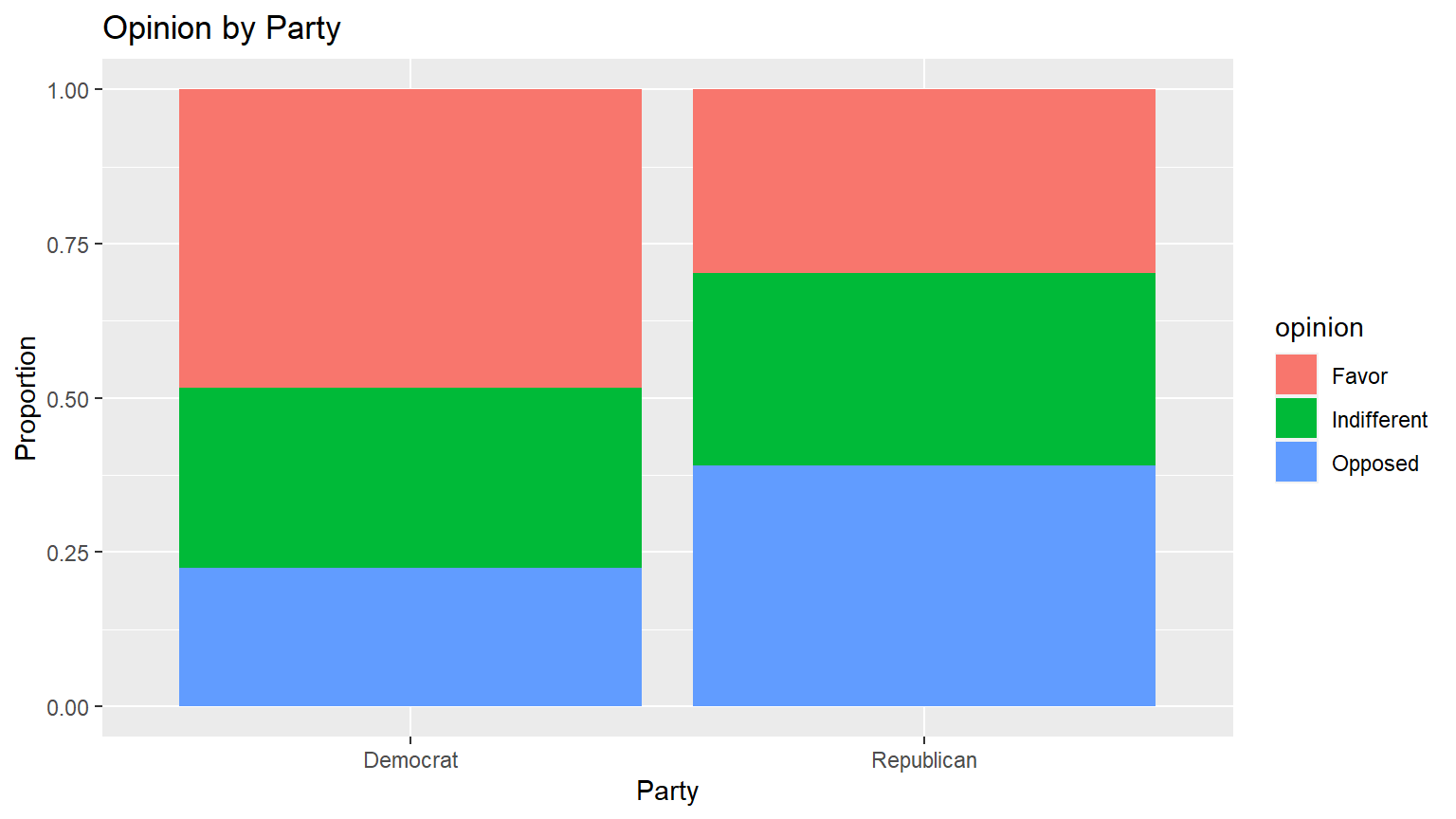

State the Null and Alternative hypotheses

Null Hypothesis, Ho: There is no relationship between political party and opinion on a tax reform bill.

Alternative Hypothesis, Ha: There is a relationship between political party and opinion on a tax reform bill.

State the Significance Level

Remember it is important to set the significance level “alpha” before starting the analysis.

Let’s set the significance level “alpha” at 5% ( i.e., 0.05) here because nothing too serious will happen if we are wrong.

Testing the hypothesis

Step 1: Calculate the statistic for the observed difference

We will again be using the Pearson Chi-squared test statistic.

CC19

delta_obs <- tax500 %>%
  specify(formula = party ~ opinion) %>% 
  hypothesize(null = "independence") %>%
  calculate(stat = "Chisq")

#display delta_obs
delta_obs

## Response: party (factor)
## Explanatory: opinion (factor)
## Null Hypothesis: independence
## # A tibble: 1 × 1
##    stat
##   <dbl>
## 1  22.2

Step 2: Generate the Null Distribution

Generate the null distribution of delta.

Here you need to generate simulated values as if we lived in a world where there’s no difference in SAT scores between high school students with low and high GPAs.

Note that this chunk is similar to CC9 but we are using the names of the variables of interest in Q2.

CC20

#set seed for reproducibilty
set.seed(123)

null_dist <- tax500 %>%
  specify(party ~ opinion) %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000, type = "permute")

Step 3: Calculate the Null difference

CC21

null_delta <- null_dist %>%
  calculate(stat = "Chisq")

Step 4: Visualize the Null Delta and the Delta Observed

CC22

visualize(null_delta) +
  shade_p_value(obs_stat = delta_obs, direction = "greater")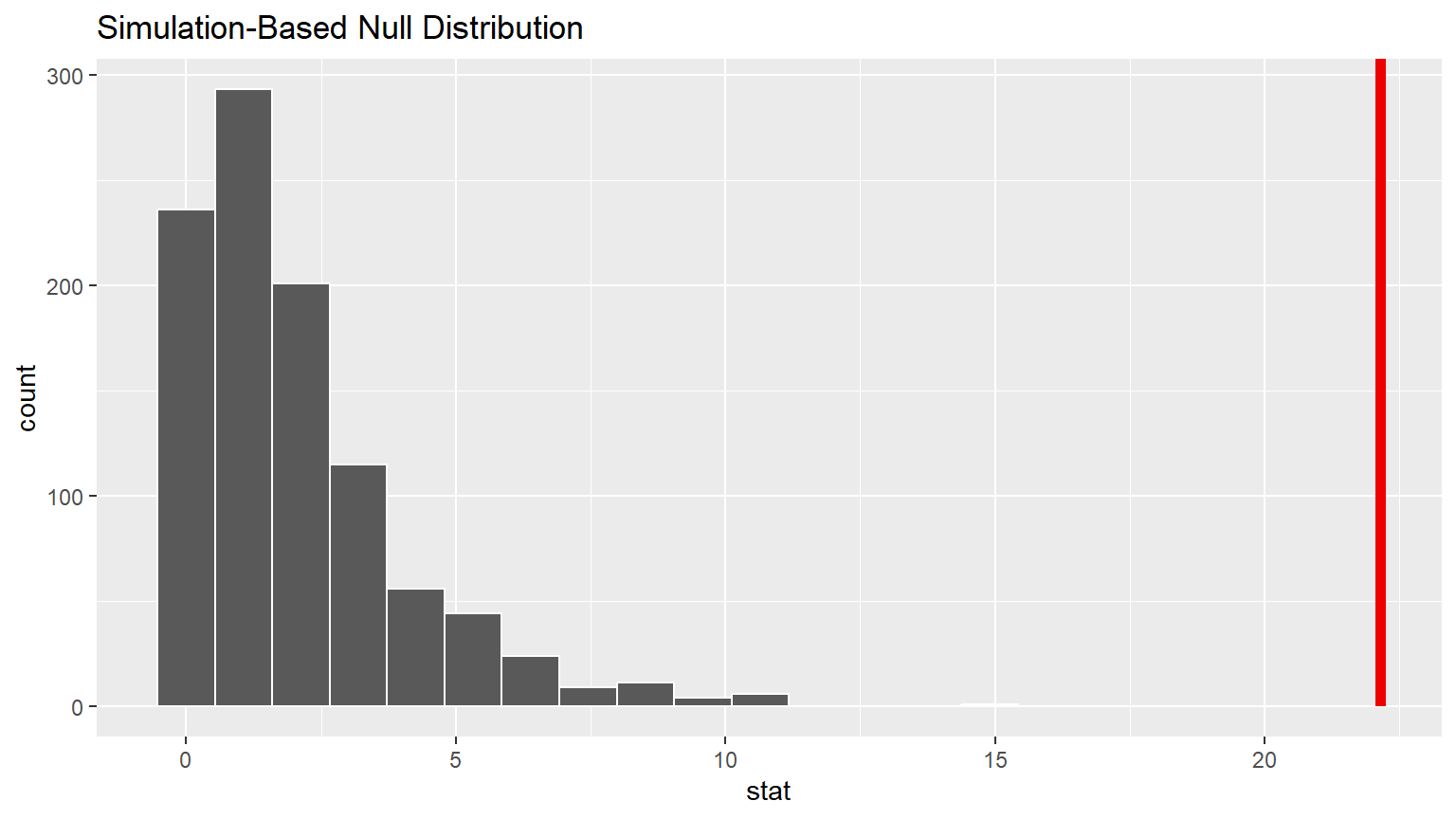

Step 5: Calculate the p-value

CC23

null_delta %>% 
  get_pvalue(obs_stat = delta_obs, direction = "greater")

## # A tibble: 1 × 1
##   p_value
##     <dbl>
## 1       0

Step 6: Results & Conclusions

Write up the results & conclusions for this hypothesis test.

Answer: The observed Chi-square test statistic is 22.15, which falls in the extreme right tail of the distribution. This result is statistically significant at alpha = 0.05, (p = < 0.01).

Based on this sample, we have sufficient evidence that the party and opinion variables are not independent. The respondent’s party did impact their opinion on the tax bill.

Step 7: Traditional Method

Use a traditional Chi-square test to test the null hypothesis that there is no relationship between political party and opinion on a tax reform bill.

CC24

tax500 %>%
  chisq_test(formula = party ~ opinion)

## # A tibble: 1 × 3
##   statistic chisq_df   p_value
##       <dbl>    <int>     <dbl>
## 1      22.2        2 0.0000155

Again, the traditional test produces essentially the same results but they should not be used until the required assumptions are checked and verified.

Lab Assignment Submission

Important

When you are ready to create your final lab report, save the Lab-07-Rehearse2-Worksheet.Rmd lab file and then Knit it to PDF or Word to make a reproducible file. This image shows you how to select the knit document file type.

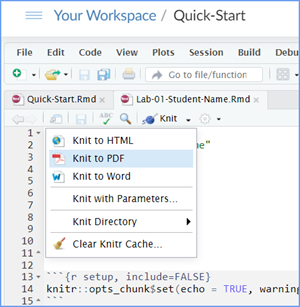
Note that if you have difficulty getting the documents to Knit to either Word or PDF, and you cannot fix it, just save the completed worksheet and submit your .Rmd file.

Ask your instructor to help you sort out the issues if you have time.

Submit your file in the Canvas M7.2 Lab 7 Rehearse(s): Hypothesis Tests Part 2 - Proportions assignment area.

The Lab 7 Hypothesis Tests Part 2 Grading Rubric will be used.

Congrats! You have finished Rehearse 2 of Lab 7. Now go to the Remix!

Previous: Lab 7 Rehearse 1

Next: Lab 7 Remix

Lab Manual Homepage

This work was created by Dawn Wright and is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

V2.0 Date 10/10/23 Last Compiled 2023-10-18

Lab 7 Rehearse 2 Version 2

Samples with Multiple Proportions

Link to Posit Cloud

Samples with Multiple Proportions

Introduction

One Categorical Variable: Goodness of Fit Test

Load Packages

Get Familiar with the Data

Load the data

Exploratory data analysis

Find unique colors of candy

Find the counts

Find the proportions

Visualize the data

State the Null and Alternative hypotheses

State the Significance Level

Testing the hypothesis

Step 1: Calculate the observed statistic

Step 2: Generate the Null Distribution

Step 3: Calculate the Null difference

Step 4: Visualize the Null and the Delta

Step 5: Calculate the p-value

Step 6: Results and Conclusions

Step 7: Calculate confidence interval

Step 8: Traditional hypothesis test

Two Categorical Variables: Test for Independence

Load Packages

Get Familiar with the Data

Load the data

Exploratory data analysis

Find the counts

Find the proportions

Visualize the Data

State the Null and Alternative hypotheses

State the Significance Level

Testing the hypothesis

Step 1: Calculate the statistic for the observed difference

Step 2: Generate the Null Distribution

Step 3: Calculate the Null difference

Step 4: Visualize the Null Delta and the Delta Observed

Step 5: Calculate the p-value

Step 6: Results & Conclusions

Step 7: Traditional Method

Lab Assignment Submission