Lab 3 Remix and Report
Distributions and Sampling
Click this Link to return to your previously deployed Posit Cloud Lab 3 Workspace:
Link to Posit Cloud
Open the “Lab 3 Distributions and Sampling” project.
Use of Generative AI Tools
Use of generative AI tools for this assignment is limited to your getting help debugging (fixing errors) or explaining code.
You may not use Gen AI to create entire code blocks/chunks.
You may not use Gen AI to generate conclusions based on analysis of a dataset.
You may not use Gen AI to write your answer to reflection questions which are usually indicated by this icon:
.You must cite your use of Gen AI using this APA guidance: Citing generative AI in APA Style
Remember to check the Lab Manual Resources Page for additional “How to” videos on this assignment.
IMPORTANT!
Open the Lab3-Remix-Student-Name.Rmd report template file in your RStudio Cloud Lab 3 Distributions and Sampling workspace.
Remember to rename this file to include your name in place of Student-Name, e.g. “Lab3-Remix-Wright-Dawn.Rmd”
Do not change anything in the yaml head space at the top
of the worksheet other than entering your name to replace Student Name
and changing the date to the current date.
Load the libraries!
The code is in the report template, so just run it.
library(ggplot2)
library(tidyverse)
library(moderndive)
library(scales)
We are going to set the random
number generator seed to a different value than in Rehearse 2. This may
mean you get different values when you run code chunks later in this
Remix.
# Set output digit precision
options(scipen = 99, digits = 3)
# Set random number generator see value for replicable pseudorandomness
set.seed(75)Remix
In section 3.2.2 Virtual Sampling of Lab 3 Rehearse 2, we took virtual samples with three different sample sizes: 25, 50, and 100.
For this Remix, select a sample size between 10 and 90, not using the 25 or 50 sample sizes, and then rerun the code using your new sample size.
You need to edit the code chunk below, carefully replacing every instance of XX in the chunk with your chosen sample size.
# Segment 1: sample size = XX
# 1.a) Virtually use shovel 1000 times
virtual_samples_XX <- bowl %>%
rep_sample_n(size = XX, reps = 1000)
# 1.b) Compute resulting 1000 replicates of proportion red
virtual_prop_red_XX <- virtual_samples_XX %>%
group_by(replicate) %>%
summarize(red = sum(color == "red")) %>%
mutate(prop_red = red / XX)
# 1.c) Plot distribution via a histogram
ggplot(virtual_prop_red_XX, aes(x = prop_red)) +
geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
labs(x = "Proportion of XX balls that were red", title = "25") Run the code several times paying attention to the shape and approximate center of the histogram each time.
Q1.
What is the approximate mean proportion of the histogram for your sample size of XX?
Your answer here:Q2.
How does the variation - shape - of the histogram differ from the shape of the original n = 100 sample size?
Here is CC10 from Lab 3 Rehearse 2 which plots the histogram for a sample size of n = 100. Do not make any changes to this code chunk. Just run it as is.
# CC10 Lab 3 Rehearse 2 - Run with no changes
# Segment 3: sample size = 100 ------------------------------
# 3.a) Virtually using shovel with 100 slots 1000 times
virtual_samples_100 <- bowl %>%
rep_sample_n(size = 100, reps = 1000)
# 3.b) Compute resulting 1000 replicates of proportion red
virtual_prop_red_100 <- virtual_samples_100 %>%
group_by(replicate) %>%
summarize(red = sum(color == "red")) %>%
mutate(prop_red = red / 100)
# 3.c) Plot distribution via a histogram
ggplot(virtual_prop_red_100, aes(x = prop_red)) +
geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
labs(x = "Proportion of 100 balls that were red", title = "100")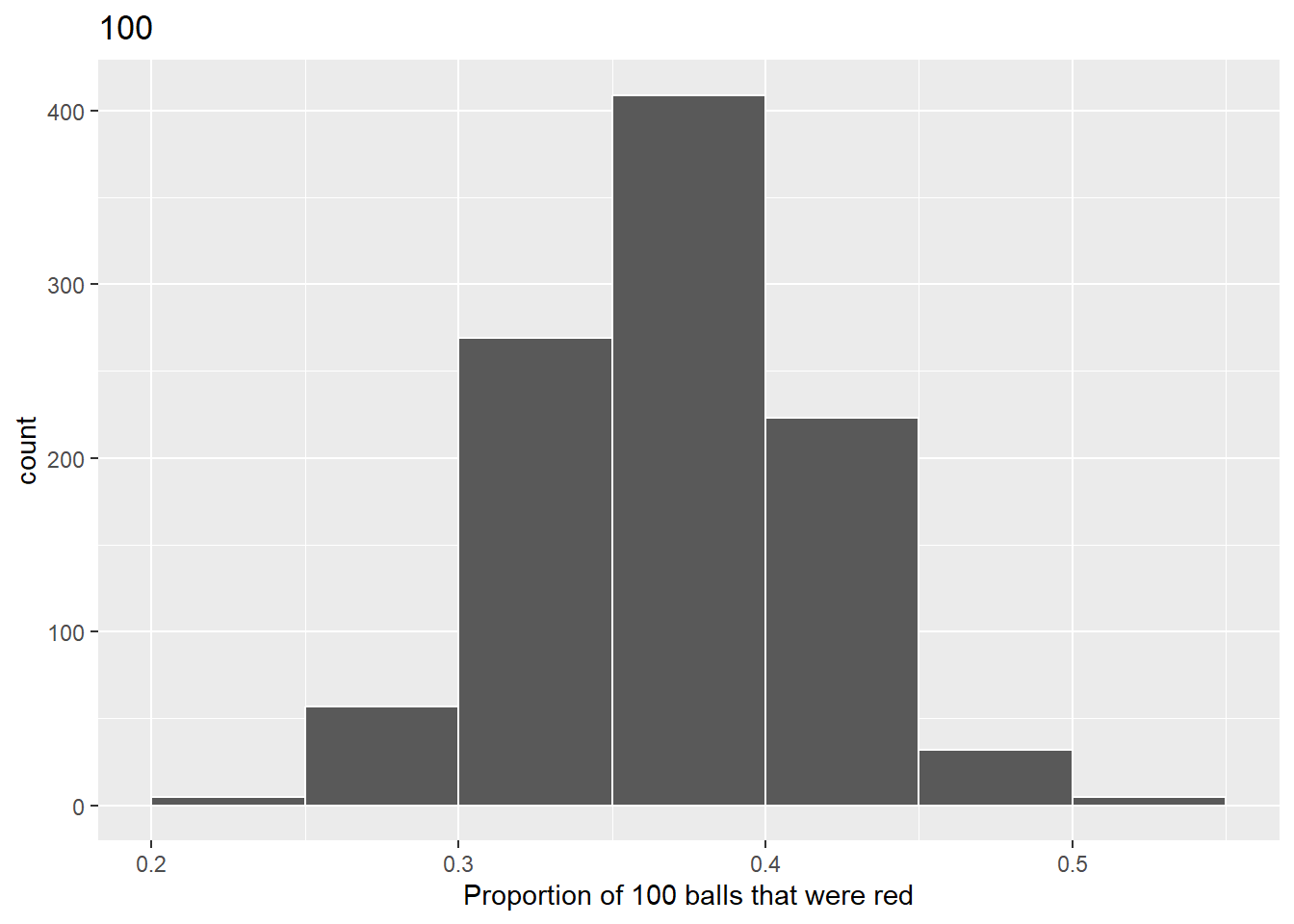 
To calculate the standard deviation for sample size n = 100, rerun this code chunk 13 from Lab 3 Rehearse 2 section 3.2.2. Do not make any changes to this code chunk.
# CC13 Lab 3 Rehearse 2 - Run with no changes
# n = 100
virtual_prop_red_100 %>%
#summarize(sd = sd(prop_red)) %>%
summarise(mean = mean(prop_red),
sd = sd(prop_red))# A tibble: 1 × 2
mean sd
<dbl> <dbl>
1 0.375 0.0460Be sure to change every instance of “XX” comment in the code chunk below to calculate the standard deviation for your new sample size n you chose above.
# n = XX
virtual_prop_red_XX %>%
summarise(mean = mean(prop_red),
sd = sd(prop_red))Write your Q2 answer here:Z-scores
In section 3.9 of the Distribution Rehearse, we discussed z-scores. Let’s expand on this idea a bit.
One common task is to describe an observation in relation to the distribution of all the observations. You can do this by finding the z-score. If you convert individual observations to z-scores, you can compare observations from different distributions.
Times for 5k and 10k runs are approximately normally distributed. That tells us the histogram of times is bell shaped and roughly symmetrical.
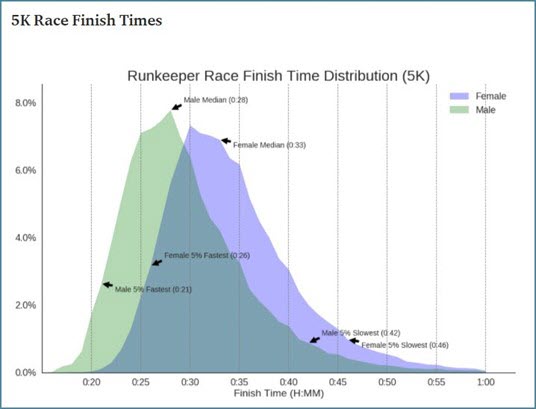
Image by Chris Drouin in Medium using Runkeeper data 2017 (Drouin, 2017)
Q3.
Lian ran a 10k race this week in 45 minutes. The mean time for women runners her age in this race was 50 minutes and the standard deviation was 5 minutes. Using the z-score formula, what is Lian’s z-score on the 10k race?
Edit the blue numbers in this code appropriately
# The 10k race
# Replace the blue-green 11, 22, and 33 in this code chunk with the appropriate values for the 10k race described above for Q3.
Lian1<-11
racemean1 <-22
racesd1 <-33
Liandifference1 <-Lian1-racemean1
Lianz1<-Liandifference1/racesd1
print(Lianz1)- 0
- -1
- +1
- -2
Your answer here:Q4.
Last week, Lian finished a 5k race in 39 minutes. The mean time for women her age for that race is 33 minutes, and the standard deviation is 3 minutes. Using the z-score formula, what is Lian’s z-score on the 5k race?
- 0
- -1
- +1
- +2
Remember to edit the blue numbers again.
# The 5k race
# Replace the blue-green 11, 22, and 33 in this code chunk with the appropriate values for the 5k race described above for Q4.
Lian2<-11
racemean2 <-22
racesd2 <-33
Liandifference2 <-Lian2-racemean2
Lian2z<-Liandifference2/racesd2
print(Lian2z)Your answer here:Q5.
On which race did Lian do the better compared to the mean time of women?
- 5k race
- 10k race
- Lian did equally well on both races.
Explain your choice.
Your answer here:Report
You answered a lot of reflection questions in the two rehearses. So, just two questions here:
Q6.
Explain the concept of sampling error.
your answer here:Q7.
Explain why the standard deviation of the sampling distribution of mean gets smaller as sample-size increases,
your answer here:** Just about done!**
As you did Labs 01 and 02, when you have edited the code chunks, you need to Knit it so see the updated graphs and tables in your final report. When you Knit an Rmarkdown file, any code chunks in it are automatically run. And all data objects in the Environment are ignored.
Lab Assignment Submission
Important
When you are ready to create your final lab report, save the
Lab-3-Remix-Your-Name.Rmd lab file. Be
sure to put your actual name in place of “Your-Name” in the file
name.
Then Knit it to a Word or PDF file. This image shows
you how to select the knit document file type.
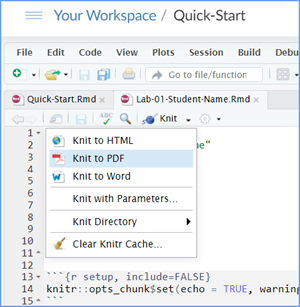
If you cannot knit to either a Word or PDF file, and you cannot fix it, just save the completed worksheet and submit your properly named (e.g. Lab-3-Remix-Susie-Smith.Rmd) file for partial credit.
Ask your instructor to help you sort out the issues if you have time.
Submit your file in the M3.4 Lab 3 Remix and Report: Sampling, Distributions and Central Limit Theorem assignment area.
The Lab 3 Grading Rubric will be used.
Congrats - you have completed Lab 3 Probability Distributions!
Previous: Lab 3 Rehearse 2
Sampling
This
work was created by Dawn Wright and is licensed under a
Creative
Commons Attribution-ShareAlike 4.0 International License.
V 2.2, Date 1/21/26
Last Compiled 2026-01-21